

|
ANTICHAINS ALGORITHMS |
|
An antichain is a set of
pairwise incomparable elements. In general, when a pre-order ≤ is given over a
set (for example set inclusion over a powerset), a downward-closed set is
a set S that contains all the elements x such that x ≤ y for some y ∈ S.
The maximal elements of a set S is the set ⌈S⌉ = {x ∈ S | ∀ y ∈ S: x ≤ y ⇒ y ≤ x}.
When dealing with downward-closed sets, we use the maximal elements as
a concise and canonical representation of sets. When ≤ is a partial order,
the set of maximal elements is an ≤-antichain.
Efficient antichain-based algorithms have been proposed to solve games of imperfect
information, language inclusion and universality of nondeterministic finite automata
over finite and infinite words, emptiness of alternating automata over finite and
infinifte words, LTL satisfiability and model-checking. Applications to tree automata
are currently under study. NEW The tool Alaska (Antichains for Logic, Automata and Symbolic Kripke structure Analysis) can be found here. |
|
|
Games of imperfect information |
We propose in [1] an antichain-based algorithm for solving safety games of imperfect information. We show that the algorithm can be used to solve games of imperfect information defined by (discrete-time) retcangular automata. In [2], we extend the result to omega-regular objectives and we consider randomized strategies. We give an algorithm for computing the set of states from which a player can win with probability 1 for a Büchi objective. An algorithm that constructs a winning strategy using antichains is presented in [3] for parity games with imperfect information.
|
|
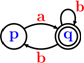
Finite word automata |
We propose in [4] antichain-based algorithms for checking universality and language inclusion for finite word automata. Experiments show excellent performances of the algorithm for universality: we can analyze automata with 5000 states while previous tools were limited to 200 states.
|

|
Infinite words and Linear Temporal Logic (LTL) |
We propose in [5] antichain-based algorithms for checking universality and language inclusion for Büchi automata. Experiments show excellent performances of the algorithm for universality: we can analyze automata with roughly 120 states while previous tools were limited to roughly 10 states. We apply these algorihms to attack the satisfiability and model-chekcing of LTL in [6].
|

|
Tree automata |
Ongoing work. |
|
People |
|
| The Verification Group at Université Libre de Bruxelles. |

|
Related works |
|

|
Other related publications |
Automata Theory
|
| Page maintained by Laurent Doyen Last update: Wed August 6 11:04 CEST 2008 |
 |
Statistics |